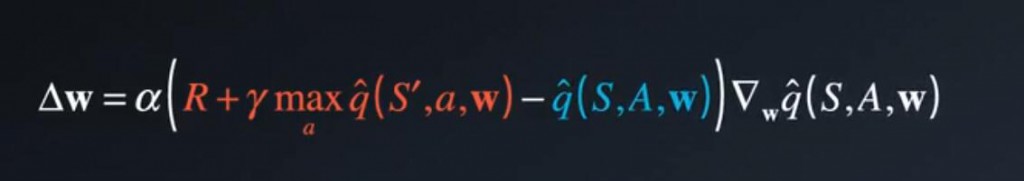
Q学习很容易受到一种联系的影响，Q学习是一种时间差分（TD）学习，这里红色部分：R + y * 下个状态的最大潜在值。称之为TD目标。

我们的目的：是缩小该目标和当前预测Q值（蓝色部分）之间的差异。

蓝色和红色部分的差异就是TD误差，这里的TD目标（红色部分）应该取代的是真值函数qπ(S,A) 。

我们不知道真值函数是什么，我们一开始使用qπ定义平方误差损失

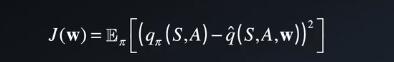
并针对w差分化，以便获得梯度下降更新规则

qπ并不依赖于我们的函数逼近器或其参数，因此形成一个简单的导数，即更新规则。但是TD目标依赖于这些参数。因此直接讲真值函数qπ替换成这样的目标，在数学上不成立。

在现实中可以忽略该问题，因为每个更新都会使参数出现小小的变化，我们基本上是朝着正确的方向前进。

下面如果将a设为1，并跳转到目标，那么可能会越过目标，并进入错误区域。此外，如果我们使用查询表或者字典，则不是什么问题，因为每个状态动作对的Q值会单独存储，但是当我们使用函数逼近时，会显著影响到学习效果。因为所有Q值都通过函数参数固定低联系到一起。

你可能会问“经验回放不会解决该问题吗？”，他解决的是有点相似，但稍微不同的问题。对于经验回访，我们通过不按顺序随机的取样元祖，打破了连续经验元祖之间的联系。但有些问题，目标和我们要更改的参数之间有联系

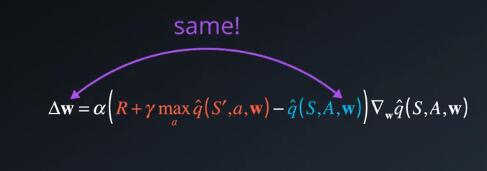
这就像追赶一个移动的目标，你永远追不到，还来回摇摆，并影响到下一个目标位置。

我们要将目标位置和追赶者分开，追赶者块追到目标时，我们再给予下一个目标，而不是

 

固定Q目标

我们也可以在Q学习中进行几乎一样的操作，将用于生成目标的函数参数固定起来，用w- 表示的固定参数，本质上是在学习过程中不会更改的w副本。在现实中，我们把w替换成w-，用他来生成目标和更改w并持续一定数量的学习步骤，然后使用最新的w更新w-，再次学习一定数量的学习步骤，循环往复。这样就可以使目标和参数拆分开来了，使学习算法更加稳定，并且不太可能会发散或者震荡。