深度卷积对抗网络简称DCGAN,这些GAN给你之前使用MNIST数据库构建差不多,但是这次的生成器和辨别器用神经网络构建,有关于DCGAN原始论文请看:https://arxiv.org/pdf/1511.06434.pdf。他的技术性不是特别强,并提供了关于这些东西训练的一些好建议。确保你在构建过程中,阅读它。
我们使用的是“街景门牌号”数据集,下图是一堆的地址图像,收集来自Google街景,他们比MNIST数据集中的图像要复杂,我们有三个颜色通道,红、绿、蓝,而且他们更大,并且图像有更多的细节。其中一些包含多个数字,那么由于这些图像比我们之前使用的,更复杂,我们需要用卷积网络来使生成器和辨别器很好的发挥作用。充分展示深度学习的神奇力量,产生一些非常酷的图像,所以基本来说,你在这里所做的和你之前在其他GAN课程中,所执行操作的唯一区别是更改生成器和辨别器。但是,训练的其余部分,像损失、优化器和输入他们基本上都一样。现在唯一的区别就在于,我们的生成器是一个卷积网络,辨别器也是一个卷积网络

那么一开始,我们和往常一样导入数据,导入模块
|
1 2 3 4 5 6 7 8 9 |
%matplotlib inline import pickle as pkl import matplotlib.pyplot as plt import numpy as np from scipy.io import loadmat import tensorflow as tf |
|
1 |
!mkdir data |
导入数据:
这部分我们加载并提取SVHN数据集。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
from urllib.request import urlretrieve from os.path import isfile, isdir from tqdm import tqdm data_dir = 'data/' if not isdir(data_dir): raise Exception("Data directory doesn't exist!") class DLProgress(tqdm): last_block = 0 def hook(self, block_num=1, block_size=1, total_size=None): self.total = total_size self.update((block_num - self.last_block) * block_size) self.last_block = block_num if not isfile(data_dir + "train_32x32.mat"): with DLProgress(unit='B', unit_scale=True, miniters=1, desc='SVHN Training Set') as pbar: urlretrieve( 'http://ufldl.stanford.edu/housenumbers/train_32x32.mat', data_dir + 'train_32x32.mat', pbar.hook) if not isfile(data_dir + "test_32x32.mat"): with DLProgress(unit='B', unit_scale=True, miniters=1, desc='SVHN Training Set') as pbar: urlretrieve( 'http://ufldl.stanford.edu/housenumbers/test_32x32.mat', data_dir + 'test_32x32.mat', pbar.hook) |
这个数据集实际上是一个.mat文件,他们通常和Matlab一起使用,但Scipy实际上有一个函数,可以将这些.mat文件,作为Numpy数组导入。那么我么们可以提取这些数组,像平常一样使用他们
|
1 2 |
trainset = loadmat(data_dir + 'train_32x32.mat') testset = loadmat(data_dir + 'test_32x32.mat') |
这里我们可以看到数据集中的一个小的图像样本
|
1 2 3 4 5 6 7 |
idx = np.random.randint(0, trainset['X'].shape[3], size=36) fig, axes = plt.subplots(6, 6, sharex=True, sharey=True, figsize=(5,5),) for ii, ax in zip(idx, axes.flatten()): ax.imshow(trainset['X'][:,:,:,ii], aspect='equal') ax.xaxis.set_visible(False) ax.yaxis.set_visible(False) plt.subplots_adjust(wspace=0, hspace=0) |

上面的图像样本,是我们即将传入辨别器的真实图像,也是生成器要学习重现的东西
|
1 2 3 4 5 6 7 8 |
def scale(x, feature_range=(-1, 1)): # scale to (0, 1) x = ((x - x.min())/(255 - x.min())) # scale to feature_range min, max = feature_range x = x * (max - min) + min return x |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
class Dataset: def __init__(self, train, test, val_frac=0.5, shuffle=False, scale_func=None): split_idx = int(len(test['y'])*(1 - val_frac)) # 构建测试集和验证集 self.test_x, self.valid_x = test['X'][:,:,:,:split_idx], test['X'][:,:,:,split_idx:] self.test_y, self.valid_y = test['y'][:split_idx], test['y'][split_idx:] self.train_x, self.train_y = train['X'], train['y'] self.train_x = np.rollaxis(self.train_x, 3) self.valid_x = np.rollaxis(self.valid_x, 3) self.test_x = np.rollaxis(self.test_x, 3) if scale_func is None: self.scaler = scale else: self.scaler = scale_func self.shuffle = shuffle def batches(self, batch_size): if self.shuffle: idx = np.arange(len(dataset.train_x)) np.random.shuffle(idx) self.train_x = self.train_x[idx] self.train_y = self.train_y[idx] n_batches = len(self.train_y)//batch_size for ii in range(0, len(self.train_y), batch_size): x = self.train_x[ii:ii+batch_size] y = self.train_y[ii:ii+batch_size] yield self.scaler(x), y |
你应该记得之前,我们的生成器使用一个tanh输入,来创建这些新的图像,以使输出的范围在-1到1之间。因此我们需要重新缩放所有真实图像,是他们在-1到1之间,以便在进入辨别器时匹配。上面就是缩放的代码,包含数据集的一个类,我们可以从batches这里获得取批。我们并不对这个网络进行分类,所以我们实际上不需要使用验证集,这只是你可以用于SVHN数据集的常规数据集的类。
网络输入
这是必不可少的。
|
1 2 3 4 5 |
def model_inputs(real_dim, z_dim): inputs_real = tf.placeholder(tf.float32, (None, *real_dim), name='input_real') inputs_z = tf.placeholder(tf.float32, (None, z_dim), name='input_z') return inputs_real, inputs_z |
我们有真实图像的输入,我们直接使用真图的尺寸,32*32*3(本例子的数据,你可以使用任意图像大小)。我只是将它留作一个占位符。
进入生成器本征向量input_z,他和我们之前在MNIST GAN中看到的一样。
生成器
这里是不同的地方,我们将在这里实现生成器和生成器的输入噪声向量z,输出也同样是一个tanh层。基本上SVHN图像输出需要匹配的大小,即32*32,但是tanh输出范围在-1到1之间。而且我们还需要匹配这些图像的深度?
我们的SVHN图像有三个颜色通道,那么他们的深度为3,即大小为32*32*3,这意味着我们具有tanh激活的输出层,也必须接受是32*32*3。这里你可以看到DCGAN论文中,使用的生成器示意图。那么(从左到右)我们取z向量,将他投射到一个全链接层,然后重塑这个全链接层,使他的大小为4*4*1024个过滤器(或者说深度),然后使用转置卷积,来减小深度并增加宽度和高度,然后在使用tanh激活。
同样在转置卷积中,使用步幅2,你会注意到这里并没有最大池化层或者类似的东西,没有全链接层。
虽然第一个使用全链接层,但是后面便全部都是卷积层,我们在转置卷积中,使用步幅2,进行所有上采样,需要注意一件事:这里最后一层在DCGAN论文中,它的大小为64*64*3,但我们的图像是32*32*3,所以他跟你应该用的架构不完全相同。但是他大致向你,展示了你应该为生成器构建的架构是什么样的。
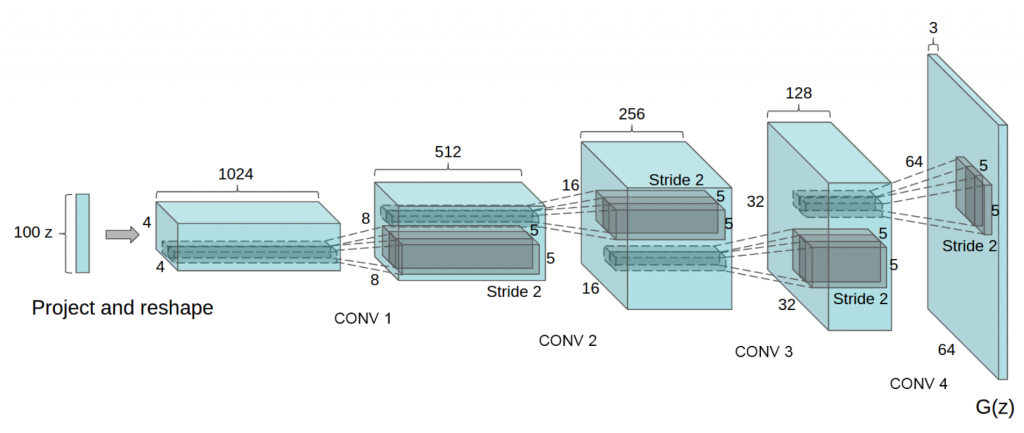
output是输出的深度,我们使用variable_scope进行重用,你也必须对上面的所有层进行批量归一化,除了最后一层,如果不使用批量归一化层,这个网络就无法发挥作用。典型的处理方式是,先使用转置卷积,然后是批量归一化,最后激活。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
def generator(z, output_dim, reuse=False, alpha=0.2, training=True): with tf.variable_scope('generator', reuse=reuse): # First fully connected layer # 首先传入张量z,这是用于生成图像噪声的向量,将他链接到一个全连接层, # 给他一个大小 4*4*512,上图前两个部分 x1 = tf.layers.dense(z, 4*4*512) # Reshape it to start the convolutional stack # 并添加批量归一化和leaky ReLU x1 = tf.reshape(x1, (-1, 4, 4, 512)) x1 = tf.layers.batch_normalization(x1, training=training) x1 = tf.maximum(alpha * x1, x1) # 4x4x512 now 上面,现在的层数为4*4*512 # 将上面的4*4*512 发到下面的转置卷积层 # 含有256个过滤器,并将步幅设为2,卷积核大小为5*5 x2 = tf.layers.conv2d_transpose(x1, 256, 5, strides=2, padding='same') # 并添加批量归一化和leaky ReLU x2 = tf.layers.batch_normalization(x2, training=training) x2 = tf.maximum(alpha * x2, x2) # 8x8x256 now x3 = tf.layers.conv2d_transpose(x2, 128, 5, strides=2, padding='same') x3 = tf.layers.batch_normalization(x3, training=training) x3 = tf.maximum(alpha * x3, x3) # 16x16x128 now # Output layer # 最后,我们连接到输出层,使用该层作为logit logits = tf.layers.conv2d_transpose(x3, output_dim, 5, strides=2, padding='same') # 32x32x3 now # 输出 out = tf.tanh(logits) return out |
我们完成的是一个转置卷积网络。
辨别器
这是我们构建辨别器的地方,同样,这与你之前看到的非常相似,我们传入真实的图像,他们是32*32*3的张量,我们让他们通过一些卷积层,最后获得sigmoid输出,我们还要返回logit。用于在sigmoid交叉熵损失函数计算中使用,这跟你之前构建的卷积分类器非常像。你可以从较宽较高的层开始,但深度仅为3。下一个卷积层会更窄一些,但也会更深,像这样将卷积层堆叠起来,卷积层越往后越窄、越深。而最后一层只是一个全连接层,你将它平滑化,所以结尾将是只有一个单元的全连接层,你将它用作sigmoid输出。对于卷积层,我建议第一层以16、32、64个过滤器开始,这是层的深度。然后对于后面的每个层,深度翻倍,而宽度和高度减半。所以基本上你每添加一个新的卷积层,就给深度乘以2,而给宽度和高度除以2 。此外,你还会需要对每一个卷积层使用leaky ReLU激活和批量归一化,要确保你不对第一层使用,批量归一化,其他层都可以。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# 这是非常普通的卷积分类器,给你之前构建的一样, # 与之前不同的是,我们这次要使用批量归一化和Leakuy ReLU # 还有这里没有最大池化,没有全连接层,结尾处除外 def discriminator(x, reuse=False, alpha=0.2): with tf.variable_scope('discriminator', reuse=reuse): # Input layer is 32x32x3 # 在第一层不要使用批量归一化,会出现一些奇怪的东西 x1 = tf.layers.conv2d(x, 64, 5, strides=2, padding='same') relu1 = tf.maximum(alpha * x1, x1) # 16x16x64 x2 = tf.layers.conv2d(relu1, 128, 5, strides=2, padding='same') bn2 = tf.layers.batch_normalization(x2, training=True) relu2 = tf.maximum(alpha * bn2, bn2) # 8x8x128 x3 = tf.layers.conv2d(relu2, 256, 5, strides=2, padding='same') bn3 = tf.layers.batch_normalization(x3, training=True) relu3 = tf.maximum(alpha * bn3, bn3) # 4x4x256 # Flatten it 我们扁平化并重塑它 # 基本上扁平化只是将它重塑为一个具有大小的长向量 # 也就是4*4*256 这是这一层的单元数量 # flat 是扁平化后层中的单元数量 flat = tf.reshape(relu3, (-1, 4*4*256)) # 我们让他通过只有一个单元的全连接层,这个单元是我们要发给sigmoid函数的输出 logits = tf.layers.dense(flat, 1) out = tf.sigmoid(logits) return out, logits |
模型损失
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
def model_loss(input_real, input_z, output_dim, alpha=0.2): """ Get the loss for the discriminator and generator :param input_real: Images from the real dataset :param input_z: Z input :param out_channel_dim: The number of channels in the output image :return: A tuple of (discriminator loss, generator loss) """ g_model = generator(input_z, output_dim, alpha=alpha) d_model_real, d_logits_real = discriminator(input_real, alpha=alpha) d_model_fake, d_logits_fake = discriminator(g_model, reuse=True, alpha=alpha) d_loss_real = tf.reduce_mean( tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_real, labels=tf.ones_like(d_model_real))) d_loss_fake = tf.reduce_mean( tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake, labels=tf.zeros_like(d_model_fake))) g_loss = tf.reduce_mean( tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake, labels=tf.ones_like(d_model_fake))) d_loss = d_loss_real + d_loss_fake return d_loss, g_loss |
优化器
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
def model_opt(d_loss, g_loss, learning_rate, beta1): """ Get optimization operations :param d_loss: Discriminator loss Tensor :param g_loss: Generator loss Tensor :param learning_rate: Learning Rate Placeholder :param beta1: The exponential decay rate for the 1st moment in the optimizer :return: A tuple of (discriminator training operation, generator training operation) """ # Get weights and bias to update t_vars = tf.trainable_variables() d_vars = [var for var in t_vars if var.name.startswith('discriminator')] g_vars = [var for var in t_vars if var.name.startswith('generator')] # Optimize with tf.control_dependencies(tf.get_collection(tf.GraphKeys.UPDATE_OPS)): d_train_opt = tf.train.AdamOptimizer(learning_rate, beta1=beta1).minimize(d_loss, var_list=d_vars) g_train_opt = tf.train.AdamOptimizer(learning_rate, beta1=beta1).minimize(g_loss, var_list=g_vars) return d_train_opt, g_train_opt |
构建模型
这里是一些用于构建模型的代码,这一次我基本上是将损失和优化器放入上面这些函数内,使这个构建过程更容易一些,这是一个叫作 GAN 的类。我们基本上在它里面构建整个模型,我们调用这些函数,构建输入,进行计算,获得损失和优化器。
我们可以用这些来实际训练网络,像这样将它打包在一个对象里,以更容易地传递数据和进行构建。
|
1 2 3 4 5 6 7 8 9 10 |
class GAN: def __init__(self, real_size, z_size, learning_rate, alpha=0.2, beta1=0.5): tf.reset_default_graph() self.input_real, self.input_z = model_inputs(real_size, z_size) self.d_loss, self.g_loss = model_loss(self.input_real, self.input_z, real_size[2], alpha=0.2) self.d_opt, self.g_opt = model_opt(self.d_loss, self.g_loss, learning_rate, beta1) |
这是用于展示正在生成的图像的一个函数,我们可以在训练过程中用它,查看进展如何。也可以在训练完成后使用它,看看是否要从生成器生成新的图像,我们可以使用此函数实际看到生成的图像。
|
1 2 3 4 5 6 7 8 9 10 11 |
def view_samples(epoch, samples, nrows, ncols, figsize=(5,5)): fig, axes = plt.subplots(figsize=figsize, nrows=nrows, ncols=ncols, sharey=True, sharex=True) for ax, img in zip(axes.flatten(), samples[epoch]): ax.axis('off') img = ((img - img.min())*255 / (img.max() - img.min())).astype(np.uint8) ax.set_adjustable('box-forced') im = ax.imshow(img, aspect='equal') plt.subplots_adjust(wspace=0, hspace=0) return fig, axes |
这个函数很明显是用来训练网络,我们只需传入网络net和数据dataset给它一些超参数,它会帮我们训练数据或训练网络。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
def train(net, dataset, epochs, batch_size, print_every=10, show_every=100, figsize=(5,5)): saver = tf.train.Saver() sample_z = np.random.uniform(-1, 1, size=(72, z_size)) samples, losses = [], [] steps = 0 with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for e in range(epochs): for x, y in dataset.batches(batch_size): steps += 1 # Sample random noise for G batch_z = np.random.uniform(-1, 1, size=(batch_size, z_size)) # Run optimizers _ = sess.run(net.d_opt, feed_dict={net.input_real: x, net.input_z: batch_z}) _ = sess.run(net.g_opt, feed_dict={net.input_z: batch_z, net.input_real: x}) if steps % print_every == 0: # At the end of each epoch, get the losses and print them out train_loss_d = net.d_loss.eval({net.input_z: batch_z, net.input_real: x}) train_loss_g = net.g_loss.eval({net.input_z: batch_z}) print("Epoch {}/{}...".format(e+1, epochs), "Discriminator Loss: {:.4f}...".format(train_loss_d), "Generator Loss: {:.4f}".format(train_loss_g)) # Save losses to view after training losses.append((train_loss_d, train_loss_g)) if steps % show_every == 0: gen_samples = sess.run( generator(net.input_z, 3, reuse=True, training=False), feed_dict={net.input_z: sample_z}) samples.append(gen_samples) _ = view_samples(-1, samples, 6, 12, figsize=figsize) plt.show() saver.save(sess, './checkpoints/generator.ckpt') with open('samples.pkl', 'wb') as f: pkl.dump(samples, f) return losses, samples |
超参
这里是你设置超参数和实际训练网络的地方,GAN 的训练稍有点复杂,因为它们对超参数非常敏感,人们不断通过各种实验,来找到最佳类型的参数,或者不是最佳的,但至少是有用的超参数。那么接下来发生的是–生成器和辨别器它们在互相玩游戏。而你必须设置超参数,以使生成器和辨别器,不会互相压制。生成器能够生成图像,而辨别器能够区分图像,确定图像是真是假。
但同时 如果辨别器的区分能力太好,生成器就无法学习。
所以你在这里要做的是尝试一些你自己的超参数,或者参阅这里的 DCGAN 论文,看看什么比较有用。我发现他们的参数对此数据库的确非常有效。但不会总是这样,当你在使用不同的数据库时,最好尝试不同的超参数。我发现的一点是,当超参数设置正确时,辨别器损失通常在 0.3 左右。这意味着:辨别器正确区分图像真假的概率为 50%,这基本上正是你想要的 对吧?
因为你想要–你的辨别器– 或你希望生成器能生成看起来逼真的图像。然后对于辨别器,如果它无法确定是真是假,则它正确的概率将是 50%,基本就像掷硬币一样。所以这就是你在设置超参数时的目标。
而且我也从我的生成器损失看到他通常在2或3之类的左右,我是说当辨别器在0.3或者0.3左右时,你可以尝试下面这些超参数。想起个好头或者一次作对,请参阅 DCGAN 论文。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
real_size = (32,32,3) z_size = 100 # 学习率为0.0002 learning_rate = 0.0002 # 批大小128 batch_size = 128 # 训练25次 epochs = 25 alpha = 0.2 beta1 = 0.5 # Create the network net = GAN(real_size, z_size, learning_rate, alpha=alpha, beta1=beta1) |
|
1 2 3 |
dataset = Dataset(trainset, testset) losses, samples = train(net, dataset, epochs, batch_size, figsize=(10,5)) |
在他训练时就一边训练一边打印,图像和生成器和辨别器损失。从一堆噪声,到可以学习颜色,到显示一些斑点,到生成类似的数字,21个echop后,可以清晰的看清出数字了,
|
1 2 3 4 5 6 |
fig, ax = plt.subplots() losses = np.array(losses) plt.plot(losses.T[0], label='Discriminator', alpha=0.5) plt.plot(losses.T[1], label='Generator', alpha=0.5) plt.title("Training Losses") plt.legend() |
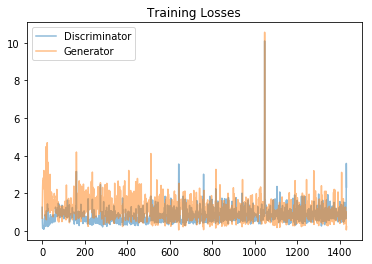
这是生成器和辨别器在训练步长中的损失图,可以看到蓝色时辨别器损失他比较低,大概在0.5左右。
|
1 2 3 4 5 6 |
fig, ax = plt.subplots() losses = np.array(losses) plt.plot(losses.T[0], label='Discriminator', alpha=0.5) plt.plot(losses.T[1], label='Generator', alpha=0.5) plt.title("Training Losses") plt.legend() |
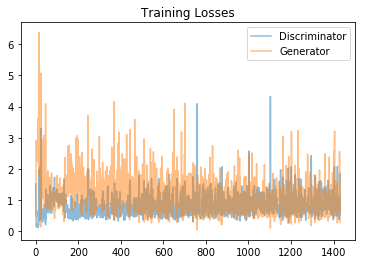
|
1 |
_ = view_samples(-1, samples, 6, 12, figsize=(10,5)) |

|
1 |
_ = view_samples(-1, samples, 6, 12, figsize=(10,5)) |

上面时我们在训练中从生成器获得的最终图像。产生了一些不错的图像,有些能清晰的看清数字。
你也可以做一些改进,这需要从Ian Goodfellow和其他人的论文中了解。