该算法中有两个交错的主要流程。

第一个流程是对环境取样，方法是执行动作，并以回放存储器的形式，存储观察的经验元祖。

环境取样

使用策略从状态S中选择动作A

执行行动A，观察奖励R和下一个输入Xt+1.

准备下一个状态

在回放存储器D中存储经验元祖（S，A，R，S‘）

S <– S”

 

学习

另一个流程是随机地从该存储器中选择一小批元祖，并使用梯度下降更新步骤从该批次中学习规律。

从D中的元祖（sj,aj,rj,sj+1）获取随机的小批次

设置目标

更新

每一个C步骤，重置 W- <—W

 

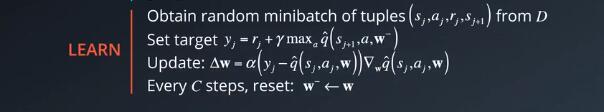
两个流程并非直接相互依赖。因此，你可以完成多个取样步骤，然后完成一个学习步骤。或者具有不同随机批次的多个学习步骤。

该算法的还有剩余步骤，旨在支持这些步骤：

1. 一开始你需要初始化空的回放存储器；注意存储器是有限的，因此你可能需要使用循环Q，保存最近的n个经验元祖。

2. 然后，你还需要初始化神经网络的参数^q或权重w;你可以采取一些不错的做法，例如，从正态分布中随机抽取一些权重方差等于每个神经元输入数量的两倍。Keras和Tensorflow等通常都包含这些初始化方法，因此不需要自己去实现这些方法。

3. 采用固定Q目标方法，你需要第二组参数 w-，它可以初始化为w。

4. （注意，这一特定算法专门用于视频游戏。）对于每个阶段和该阶段中的每个时间步t，你会观察原始屏幕图像或者输入帧Xt，并需要将其转换为灰阶形式，剪切为正方形等等。此外，为了捕获时间关系，你可以堆叠一些输入帧以构建每个状态向量，我们用函数phi表示这个预处理和堆叠操作，该函数会接收一系列的帧并形成组合表示法。注意，如果我们要堆叠帧。例如四个帧则需要对前三个时间步进行特殊处理。比如，我们可以将这些丢失的帧，当作空帧，使用第一帧的副本或跳过存储经验帧这一步，直到获得完整的序列。在现实中，你无法立即运行学习步骤，需要等待，直到存储器中有足够数量的元祖。

注意每个阶段之后，我们不清空存储器，这样可以跨阶段地回忆和形成批量经验，DQN论文中用到了很多其他技巧和优化方式，

例如奖励裁剪，误差裁剪，将过去的动作存储为状态向量的一部分，处理终止状态，挖掘一段时间内的 ∈等

 

延伸阅读：

• Mnih et al.，2015 年，《通过深度强化学习实现人类级别的控制》（DQN 论文）
• He et al. ，2015 年，《深入研究纠正器：在 ImageNet 分类方面超过人类水平》（权重初始化）