我们来看三个重要的改进：

–  双DQN

–  优先回放

–  对抗网络

双DQN

我们解决的第一个问题是：Q学习容易出现过高估计动作值问题。

我们来回顾一下具有函数逼近的Q学习更新规则，并重点看看TD目标

这里的max运算有必要用到，以便计算可以从下个状态获得最佳潜在值，为了更好的理解这一点，我们重写目标并展开max运算。可以更有效的理解为，我们想要获得状态S’的Q值，以及从该状态的所有潜在动作中实现最大Q值的动作

可以看出arg max运算有可能会出错，尤其是在早期阶段。为何？因为Q值依然在变化，我们可能没有收集足够的信息来判断最佳动作是什么，Q值的准确性在很大程度上取决于：尝试了哪些动作以及探索了哪些周围的状态。实际上，事实证明这一部分会导致过高估计Q值，因为我们始终在一组杂乱数字中选择最大值，或许我们不应该盲目的信任这些值。

那么如何才能使我们的估值更加可靠呢？有一个经实践证明效果很好的方法就是双Q学习，我们使用一组参数w，选择最佳动作，但是使用另一组参数w‘，评估动作。相当于有两个单独的函数逼近器，我们必须在最佳动作上达成一致，如果根据W‘  和W 选择的动作并不是最佳动作，那么返回的Q值不会这么高，长期下来，就可以避免该算法传播偶尔获得的更高奖励，这些奖励并不能反映长期回报。

你可能会问，我们从哪获取第二参数呢？从原始的双Q学习公式中，你会保留两个值函数，在每一步随机选择一个函数进行更新，并仅使用另一个评估动作。但是将DQN与固定Q目标结合使用时，我们已经有一组替代的参数。

还记得W-吗？实际上，W- 已经保留不用有一段时间了。它与W之间的区别已经足够大，可以重新用于该目的，原理就是这样。这个简单的修改就可以使Q值变起来可靠。防止他们在学习的早期阶段爆发或在后期阶段出现波动。经过证明，形成的策略效果比Vanilla DQN强很多。

 

优先回放

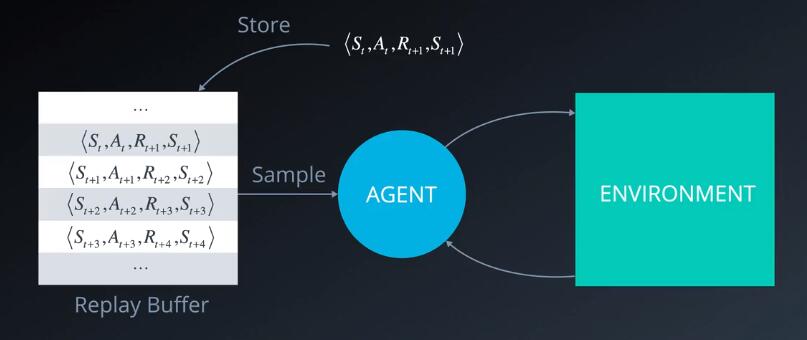
回忆一下经验回放的基本原理，我们与环境互动以便收集经验元祖，将元祖保存在缓冲区，然后随机抽取一个批次从中学习规律。这样有助于打破连续经验之间的关系。并使学习算法稳定下来，到目前为止没有发现什么问题。但是某些经验可能比其他经验更重要，更需要学习。此外，这些重要的经验可能很少发生，如果我们均匀地按照批次抽样，那么这些经验被选中的概率很小，因为缓冲区实际上容量有限。因此更早的重要经验可能会丢失，这时候就要用到优先经验回放了。

但是我们根据什么条件来为每个元祖分配优先级呢？一种方法是使用TD误差增量，误差越大，我们该元祖中预计学到的规律就越多。我们将此误差的大小作为衡量优先级的条件，并将其与每一个相应的元祖一起存储在回放缓冲区。在创建批次时，我们可以使用该值计算抽样概率。选择任何元祖i的概率等于其优先级值pi，并用回放缓冲区中的所有优先级值之和标准化。选择某个元祖后，我们可以使用最新的Q值，将其优先级更新为新计算的TD误差。似乎效果不错，经过证明，可以减少学习值函数所需的批次更新数量。

有几个方面可以加以改进。首先，如果TD误差为0，那么该元祖的优先级值及其被选中的概率也为0。

0或者非常低的TD误差，并不一定就表明我们从此类元祖中学不到任何规律，可能是因为到该时间点为止，经历的样本有限。估值很接近真实的值。为了防止此类元祖不被选中，我们可以在每个平衡值后面加上一个很小的常量e

另一个类似的问题是贪婪地使用这些优先级值，可能会导致一小部分经验子集不断被回放，导致对该子集的过拟合。为了避免该问题，我们重新引入一些均匀随机抽样元素，这样会添加另一个超参数a，我们用它将抽样概率重新定义为，优先级pi的a次幂除以所有优先级之和pk，每个都是a次幂，我们可以通过调整该参数，控制采用优先级的随机性的幅度。

a等于0，表示采用完全均匀随机性方法，a等于1，表示仅采用优先级值。当我们使用优先经验回放时，我们需要对更新规则进行一项调整

我们的原始Q学习更新，来自于对所有经验的预期结果，在使用随机性更新规则时，我们对这些经验抽样的方式，必须与来源底层分布匹配。

当我们从回放缓冲区均匀地抽样经验元祖时，能够满足这一前提条件。

但当我们采用非均匀抽样时（例如，使用优先级）时，则不满足该前提条件。我们学习的Q值将因为这些优先级值出现偏差。我们只希望使用这些值进行抽样，为了更正这一偏差，我们需要引入一个重要的抽样权重等于 1/N，N是该回放缓冲区的大小，乘以1/p(i) ，p(i)是抽样概率，我们可以添加另一个超参数b，并将每个重要抽样权重提升为b，控制这些权重对学习的影响程度比这些权重在学习结束是更加重要。这时候Q值开始收敛，因此你可以逐渐将b从很低的值增加到1，这些细节部分可能一开始很难明白，但是每个小小的改进，都可以有效地达到更加稳定高效的学习算法，因此确保仔细阅读优先经验回放论文。

 

对抗网络

我们将简单介绍最后一个DQN增强技巧，对抗网络。

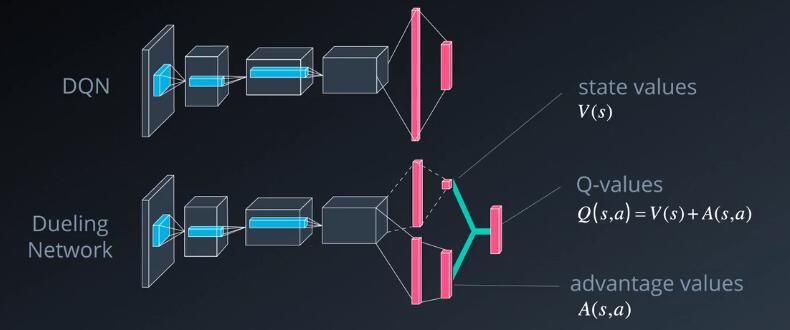
这是一个典型DQN架构，有一系列卷积层，然后是几个完全连接层，生成了Q值，对抗网络的核心概念是使用两个信息流，一个估算状态值函数，一个估值每个动作的优势，两个信息流，可能在一开始具有一些共同的层级。例如，卷积层，然后分支为各自的完全连接层，最后通过结合状态和优势值，获得期望的Q值，这么做的原因是，大部分状态在动作之间变化不大，因此可以尝试直接估算它们，但是我们依然需要捕获动作在每个状态中产生的区别，这时候我们就要用到优势函数，需要进行一些调整，以便将Q学习应用与该框架，你可以在对抗网络论文中找到该调整的方法。和双DQN以及经验回放一样，该技巧显著改善了vanilla DQN。