在此 notebook 中,我们将构建一个可以通过强化学习学会玩游戏的神经网络。具体而言,我们将使用 QQ-学习训练智能体玩一个叫做 Cart-Pole 的游戏。在此游戏中,小车上有一个可以自由摆动的杆子。小车可以向左和向右移动,目标是尽量长时间地使杆子保持笔直。
我们可以使用 OpenAI Gym 模拟该游戏。首先,我们看看 OpenAI Gym 的原理。然后,我们将训练智能体玩 Cart-Pole 游戏。
|
1 2 3 4 5 6 7 8 |
import gym import numpy as np # Create the Cart-Pole game environment env = gym.make('CartPole-v1') # Number of possible actions print('Number of possible actions:', env.action_space.n) |
[2018-01-22 23:10:02,350] Making new env: CartPole-v1
Number of possible actions: 2
我们通过 env 与模拟环境互动。你可以通过 env.action_space.n查看有多少潜在的动作,并且使用 env.action_space.sample() 获得随机动作。向 env.step 传入动作(用整数表示)将生成模拟环境的下一个步骤。所有 Gym 游戏基本都是这样。
在 Cart-Pole 游戏中有两个潜在动作,即使小车向左或向右移动。因此我们可以采取两种动作,分别表示为 0 和 1。
运行以下代码以与环境互动。
|
1 2 3 4 5 6 7 8 9 10 11 |
actions = [] # actions that the agent selects rewards = [] # obtained rewards state = env.reset() while True: action = env.action_space.sample() # choose a random action state, reward, done, _ = env.step(action) rewards.append(reward) actions.append(action) if done: break |
我们可以查看动作和奖励:
|
1 2 |
print('Actions:', actions) print('Rewards:', rewards) |
Actions: [0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0]
Rewards: [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0]
当杆子倾斜角度超过特定的角度之后,游戏就会重置。当游戏还在运行时,在每一步都会返回奖励 1.0。游戏运行时间越久,我们获得的奖励就越多。网络的目标是通过使杆子保持垂直状态最大化奖励。为此,它将使小车向左和向右移动。
Q-网络
为了跟踪动作值,我们将使用接受状态 ss 作为输入的神经网络。输出将是每个潜在动作的 QQ 值(即输出是输入状态 ss 对应的所有动作值 Q(s,a)Q(s,a)。
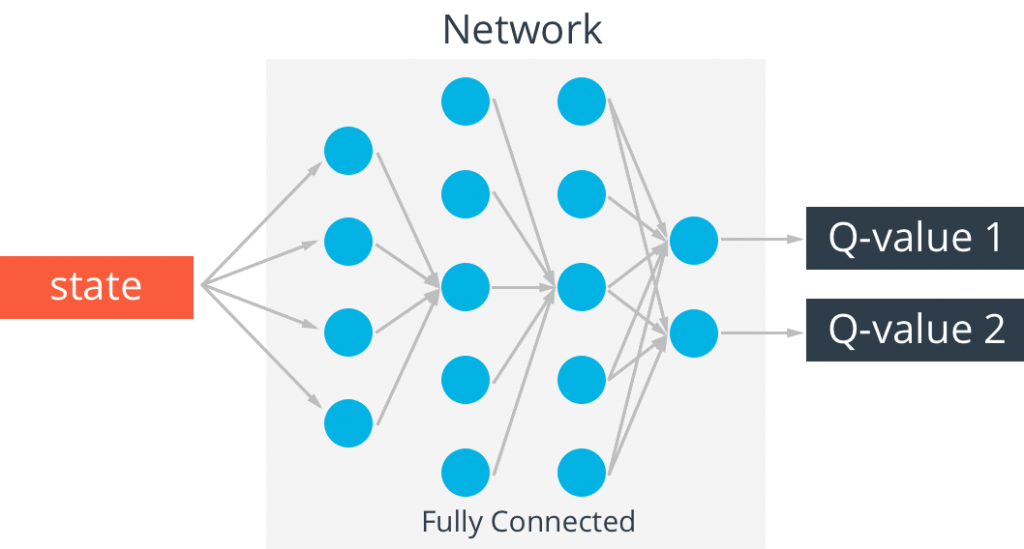
对于这个 Cart-Pole 游戏,状态有四个值:小车的位置和速度,杆子的位置和速度。因此,该神经网络有四个输入(状态中的每个值对应一个输入)和两个输出(每个潜在动作对应一个输出)。
正如在这节课所讨论的,为了实现训练目标,我们首先将利用状态 ss 提供的背景信息选择动作 aa,然后使用该动作模拟游戏。这样将会获得下个状态 s′s′ 以及奖励 rr。这样我们就可以计算 Q̂ (s,a)=r+γmaxa′Q(s′,a′)。然后,我们通过最小化 (Q̂ (s,a)−Q(s,a))2(2是平方) 更新权重。
下面是 Q 网络的一种实现。它使用两个包含 ReLU 激活函数的完全连接层。两层似乎很好,三层可能更好,你可以随意尝试。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
import tensorflow as tf class QNetwork: def __init__(self, learning_rate=0.01, state_size=4, action_size=2, hidden_size=10, name='QNetwork'): # state inputs to the Q-network with tf.variable_scope(name): self.inputs_ = tf.placeholder(tf.float32, [None, state_size], name='inputs') # One hot encode the actions to later choose the Q-value for the action self.actions_ = tf.placeholder(tf.int32, [None], name='actions') one_hot_actions = tf.one_hot(self.actions_, action_size) # Target Q values for training self.targetQs_ = tf.placeholder(tf.float32, [None], name='target') # ReLU hidden layers self.fc1 = tf.contrib.layers.fully_connected(self.inputs_, hidden_size) self.fc2 = tf.contrib.layers.fully_connected(self.fc1, hidden_size) # Linear output layer self.output = tf.contrib.layers.fully_connected(self.fc2, action_size, activation_fn=None) ### Train with loss (targetQ - Q)^2 # output has length 2, for two actions. This next line chooses # one value from output (per row) according to the one-hot encoded actions. self.Q = tf.reduce_sum(tf.multiply(self.output, one_hot_actions), axis=1) self.loss = tf.reduce_mean(tf.square(self.targetQs_ - self.Q)) self.opt = tf.train.AdamOptimizer(learning_rate).minimize(self.loss) |
经验回放
强化学习算法可能会因为状态之间存在关联性而出现稳定性问题。为了在训练期间减少关联性,我们可以存储智能体的经验,稍后从这些经验中随机抽取一个小批量经验进行训练。
在以下代码单元格中,我们将创建一个 Memory 对象来存储我们的经验,即转换 <s,a,r,s′>。该存储器将设有最大容量,以便保留更新的经验并删除旧的经验。然后,我们将随机抽取一个小批次转换 <s,a,r,s′> 并用它来训练智能体。
我在下面实现了 Memory 对象。如果你不熟悉 deque,其实它是一个双端队列。可以将其看做在两端都有开口的管子。你可以从任何一端放入物体。但是如果放满了,再添加物体的话将使物体从另一端被挤出。这是一种非常适合内存缓冲区的数据结构。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
from collections import deque class Memory(): def __init__(self, max_size=1000): self.buffer = deque(maxlen=max_size) def add(self, experience): self.buffer.append(experience) def sample(self, batch_size): idx = np.random.choice(np.arange(len(self.buffer)), size=batch_size, replace=False) return [self.buffer[ii] for ii in idx] |
Q-学习训练算法
我们将使用以下算法训练网络。对于此游戏,目标是使杆子在 195 帧内都保持垂直状态。因此当我们满足该目标后,可以开始新的阶段。如果杆子倾斜角度太大,或者小车向左或向右移动幅度太大,则游戏结束。当游戏结束后,我们可以开始新的阶段。现在,为了训练智能体:
- 初始化存储器 D
- 使用随机权重初始化动作值网络 Q
- 对于阶段 ←1 到 M,执行以下操作
- 观察 s0
- 对于 t←0 到 T−1,执行以下操作
- 对于概率 ϵ,选择随机动作 at,否则选择 at=argmaxaQ(st,a)
- 在模拟器中执行动作 at,并观察奖励 rt+1 和新状态 st+1
- 将转换 <st,at,rt+1,st+1> 存储在存储器 D 中
- 从 D: <sj,aj,rj,s′j> 中随机抽取小批量经验
- 如果阶段在 j+1时结束,设为 Q̂ j=rj,否则设为 Q̂ j=rj+γ max a′Q(s′j,a′)
- 创建梯度下降步骤,损失为 (Q̂ j−Q(sj,aj))2(平方)
- endfor
- endfor
建议你花时间扩展这段代码,以实现我们在这节课讨论的一些改进之处,从而包含固定 QQ目标、双 DQN、优先回放和/或对抗网络。
超参数
对于强化学习,比较难的一个方面是超参数很大。我们不仅要调整网络,还要调整模拟环境。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
train_episodes = 1000 # max number of episodes to learn from max_steps = 200 # max steps in an episode gamma = 0.99 # future reward discount # Exploration parameters explore_start = 1.0 # exploration probability at start explore_stop = 0.01 # minimum exploration probability decay_rate = 0.0001 # exponential decay rate for exploration prob # Network parameters hidden_size = 64 # number of units in each Q-network hidden layer learning_rate = 0.0001 # Q-network learning rate # Memory parameters memory_size = 10000 # memory capacity batch_size = 20 # experience mini-batch size pretrain_length = batch_size # number experiences to pretrain the memory |
未完待续中。。。。